Научно-образовательный портал
W-10.RU

On a decomposition of an element of a free metabelian group as a productof primitive elements

On a decomposition of an element of a free metabelian group as a productof primitive elements

On a decomposition of an element of a free metabelian group as a productof primitive elements

E.G. Smirnova, Omsk State University, Mathematical Department

1. Introduction

Let G=Fn/V be a free in some variety group of rank n. An element is called primitive if and only if g can be included in some basis g=g1,g2,...,gn of G. The aim of this note is to consider a presentation of elements of free groups in abelian and metabelian varieties as a product of primitive elements. A primitive length |g|pr of an element is by definition a smallest number m such that g can be presented as a product of m primitive elements. A primitive length |G|pr of a group G is defined as , so one can say about finite or infinite primitive length of given relatively free group.

Note that |g|pr is invariant under action of Aut G. Thus this notion can be useful for solving of the automorphism problem for G.

This note was written under guideness of professor V. A. Roman'kov. It was supported by RFFI grant 95-01-00513.

2. Presentation of elements of a free abelian group of rank n as a product of primitive elements

Let An be a free abelian group of rank n with a basis a1,a2,...,an. Any element can be uniquelly written in the form

.

Every such element is in one to one correspondence with a vector . Recall that a vector (k1,...,kn) is called unimodular, if g.c.m.(k1,...,kn)=1.

Лемма 1. An element of a free abelian group An is primitive if and only if the vector (k1,...,kn) is unimodular.

Доказательство. Let , then . If c is primitive, then it can be included into a basis c=c1,c2,...,cn of the group An. The group (n factors) in such case, has a basis , where means the image of ci. However, , that contradics to the well-known fact: An(d) is not allowed generating elements. Conversely, it is well-known , that every element c=a1k1,...,ankn such that g.c.m.(k1,...,kn)=1 can be included into some basis of a group An.

Note that every non unimodular vector can be presented as a sum of two unimodular vectors. One of such possibilities is given by formula (k1,...,kn)=(k1-1,1,k3,...,kn)+(1,k2-1,0,...,0).

Предложение 1. Every element , , can be presented as a product of not more then two primitive elements.

Доказательсво. Let c=a1k1...ankn for some basis a1,...an of An. If g.c.m.(k1,...,kn)=1, then c is primitive by Lemma 1. If , then we have the decomposition (k1,...,kn)=(s1,...,sn)+(t1,...,tn) of two unimodular vectors. Then c=(a1s1...ansn)(a1t1...antn) is a product of two primitive elements.

Corollary.It follows that |An|pr=2 for . ( Note that .

3. Decomposition of elements of the derived subgroup of a free metabelian group of rank 2 as a product of primitive ones

Let be a free metabelian group of rank 2. The derived subgroup M'2 is abelian normal subgroup in M2. The group is a free abelian group of rank 2. The derived subgroup M'2 can be considered as a module over the ring of Laurent polynomials

.

The action in the module M'2 is determined as ,where is any preimage of element in M2, and

.

Note that for , we have

(u,g)=ugu-1g-1=u1-g.

Any automorphism is uniquelly determined by a map

.

Since M'2 is a characteristic subgroup, induces automorphism of the group A2 such that

Consider an automorphism of the group M2, identical modM'2, which is defined by a map

,

By a Bachmuth's theorem from [1] is inner, thus for some we have

Consider a primitive element of the form ux, . By the definition there exists an automorphism such that

Using elementary transformations we can find a IA-automorphism with a first row of the form(1). Then by mentioned above Bachmuth's theorem

In particular the elements of type u1-xx, u1-yy, are primitive.

Предложение 2. Every element of the derived subgroup of a free metabelian group M2 can be presented as a product of not more then three primitive elements.

Доказательство. Every element can be written as , and can be presented as

.

Thus,

A commutator , by well-known commutator identities can be presented as

The last commutator in (3) can be added to first one in (2). We get [y-1 , that is a product of three primitive elements.

4. A decomposition of an element of a free metabelian group of rank 2 as a product of primitive elements

For further reasonings we need the following fact: any primitive element of a group A2 is induced by a primitive element , . It can be explained in such way. One can go from the basis to some other basis by using a sequence of elementary transformations, which are in accordance with elementary transformations of the basis <x,y> of the group M2.

The similar assertions are valid for any rank .

Предложение 3. Any element of group M2 can be presented as a product of not more then four primitive elements.

Доказательство. At first consider the elements in form . An element is primitive in A2 by lemma 1, consequently there is a primitive element of type . Hence, Since, an element is primitive, it can be included into some basis inducing the same basis of A2. After rewriting in this new basis we have:

,

and so as before

Obviously, two first elements above are primitive. Denote them as p1, p2. Finally, we have

, a product of three primitive elements.

If , then by proposition 1 we can find an expansion as a product of two primitive elements, which correspond to primitive elements of M2: v1xk1yl1,v2xk2yl2,v1,v2 .

Further we have the expansion

The element w(v1xk1yl1) can be presented as a product of not more then three primitive elements. We have a product of not more then four primitive elements in the general case.

5. A decomposition of elements of a free metabelian group of rank as a product of primitive elements

Consider a free metabelian group Mn=<x1,...,xn> of rank .

Предложение 4. Any element can be presented as a product of not more then four primitive elements.

Доказательсво. It is well-known [2], that M'n as a module is generated by all commutators . Therefore, for any there exists a presentation

Separate the commutators from (4) into three groups in the next way.

1) - the commutators not including the element x2 but including x1.

2) - the other commutators not including the x1.

3) And the third set consists of the commutator .

Consider an automorphism of Mn, defining by the following map:

,

.

The map determines automorphism, since the Jacobian has a form

,

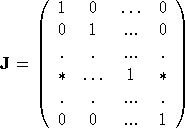
and hence, det Jk=1.

Since element can be included into a basis of Mn, it is primitive. Thus any element can be presented in form

x3x2x1]

[x1-1x2-1x3-1]. =p1p2p3p4 a product of four primitive elements.

Note that the last primitive element p4=x1-1x2-1x3-1 can be arbitrary.

Предложение 5. Any element of a free metabelian group Mn can be presented as a product of not more then four primitive elements.

Доказательство. Case 1. Consider an element , so that g.c.m.(k1,...,kn)=1. An element is primitive by lemma 1 and there exists a primitive element ,

An element from derived subgroup can be presented as a product of not more then four primitive elements with a fixed one of them:

Then .

Case 2. If , then by lemma 2 , where are primitive in An. There exist primitive elements So We have just proved that the element wp1 can be presented as a product of not more then three primitive elements p1'p2'p3'. Finally we have c=p1'p2'p3'p2, a product of not more then four primitive elements.

Список литературы

Bachmuth S. Automorphisms of free metabelian groups // Trans.Amer.Math.Soc. 1965. V.118. P. 93-104.

Линдон Р., Шупп П. Комбинаторная теория групп. М.: Мир, 1980.

Для подготовки данной работы были использованы материалы с сайта http://www.omsu.omskreg.ru/